树状数组模板程序讲解2（超详细）

Andy

> 本文主要介绍和解释树状数组的**区间修改**和**单点查询**的模板
> 区间修改和单点查询请看https://blog.csdn.net/a_n_d_y_s_u_n__/article/details/119610734


## 模板题目：
- 题目链接https://www.luogu.com.cn/problem/P3368




## 模板代码：

本题需要用到差分思想，如果不会可以先在[这里](https://blog.csdn.net/a_n_d_y_s_u_n__/article/details/119615494)学习，否则很难理解本题做法（而且差分经常和树状数组一起出现）

为了方便你对程序的理解，可以在不太清楚的地方结合此图思考一下，能节约思考时间。




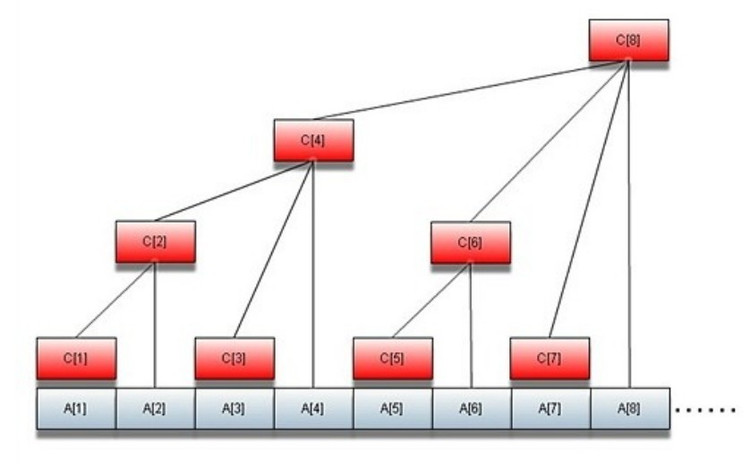
讲解请看代码注释

[C++] 纯文本查看 复制代码

#include<iostream>
#include<cstdio>
#define reint register int
using namespace std;
int f[2000001],n,b[2000001]; //f用来维护差分数组的前缀和（也就是记录每一次修改对原数组造成的影响），b是数组初始数值
int lowbit(int a) {  //lowbit函数，用来计算a在二进制下从右往左第一个`1`出现的位置（其实说白了就是用来跳转到f中和a有关的变量，实在不懂记住就可以，不用在这里浪费时间）
        return a&-a;   //计算方法，等同于a&(a^(a-1))
}
void add(int x,int k) {  //把第x个数加上k
        while(x<=n) {   //如果没有越界就一直循环
                f[x]+=k;  //把第x个数加上k
                x+=lowbit(x);  //跳转代码，快速找到包含了f[x]的所有前缀和
        }
        return;
}
int sum(int x) {  //用来计算差分数组的前缀和
        int ans(0);   //累加变量
        while(x>0) {   //如果没有越界就一直循环
                ans+=f[x];    //累加前缀和
                x-=lowbit(x);   //lowbit跳转
        }
        return ans;  //返回ans
}
int main() {
        int i,m;
        cin>>n>>m;
        for(i=1; i<=n; ++i) {
                scanf("%d",&b[i]);  //输入初始数据
        }
        for(i=1; i<=m; ++i) {
                int p,x,y,z;
                scanf("%d",&p);
                if(p==1) {
                        scanf("%d%d%d",&x,&y,&z);
                        add(x,z);  //差分思想，具体见上面链接
                        add(y+1,-z);  //差分思想
                } else {
                        scanf("%d",&x);
                        printf("%d\n",sum(x)+b[x]);  //用多次修改后造成的影响+数组初始值就是改变后的值
                }
        }
}[/i]
[i]

------


如果还有其他问题可以在下方留言，也可以在https://blog.csdn.net/a_n_d_y_s_u_n__/article/details/119534584寻找其他更适合适合你的教程~